


Next: 3.3 A Survey of
Up: 3 The Topological Point
Previous: 3.1 Flexible Curves
3.2 The Most Elementary Prohibitions on Real Topology of a
Flexible Curve
The simplest prohibitions
are not related to the position of
 in
in
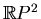 , but
deal with the following purely topological situation: a
surface
, but
deal with the following purely topological situation: a
surface 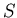 , which is homeomorphic to a sphere with
, which is homeomorphic to a sphere with
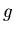 (
(
 ) handles,
and an involution
) handles,
and an involution  (
( ) of
) of 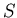 reversing orientation with
fixed point set
reversing orientation with
fixed point set 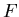 (
(
 ).
).
The most important of these prohibitions is Harnack's inequality.
Recall that it is
where 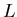 is the number of connected components of the real part
a curve and
is the number of connected components of the real part
a curve and 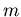 is its degree. Certainly, this formulation given in
Section 1.3 can be better adapted to the context of flexible
curves. The number
is its degree. Certainly, this formulation given in
Section 1.3 can be better adapted to the context of flexible
curves. The number
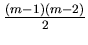 is nothing but the genus.
Therefore the Harnack inequality follows from the following theorem.
is nothing but the genus.
Therefore the Harnack inequality follows from the following theorem.
3.2.A
For a
reversing orientation involution
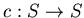
of a sphere
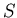
with
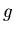
handles, the number
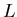
of connected components of the fixed point
set
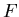
is at most
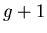
.
In turn, 3.2.A can be deduced from the following purely
topological theorem on involutions:
3.2.B Smith-Floyd Theorem.
For any involution
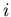
of a topological space
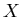
,
This theorem is one of the most famous results of the Smith theory. It
is deduced from the basic facts on equivariant homology of involution,
see, e. g., [Bre-72, Chapter 3].
Theorem 3.2.A follows from 3.2.B, since
and
Smith - Floyd Theorem can be applied to high-dimensional situation, too.
See Sections 5.3 and ![[*]](/usr/share/latex2html/icons/crossref.png) . In the one-dimensional case,
which we deal with here,
Theorem 3.2.B is easy to
prove without any homology tool, like the Smith theory. Namely, consider
the orbit space
. In the one-dimensional case,
which we deal with here,
Theorem 3.2.B is easy to
prove without any homology tool, like the Smith theory. Namely, consider
the orbit space 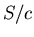 of the involution. It is a connected surface with
boundary. The boundary is the image of the fixed point set. The Euler
characteristic of the orbit space is equal to the half of the Euler
characteristic of
of the involution. It is a connected surface with
boundary. The boundary is the image of the fixed point set. The Euler
characteristic of the orbit space is equal to the half of the Euler
characteristic of 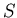 , i.e. it is
, i.e. it is
 . Cap each boundary
circle with a disk. The result is a closed connected surface with Euler
characteristic
. Cap each boundary
circle with a disk. The result is a closed connected surface with Euler
characteristic  . On the other hand, as it is well known,
the Euler characteristic of a connected closed surface is at most
2. (Remind that such a surface is homeomorphic either to the sphere,
which has
Euler characteristic 2, or the sphere with
. On the other hand, as it is well known,
the Euler characteristic of a connected closed surface is at most
2. (Remind that such a surface is homeomorphic either to the sphere,
which has
Euler characteristic 2, or the sphere with  handles, whose Euler
characteristic is
handles, whose Euler
characteristic is  , or sphere with
, or sphere with  Möbius strips having
Euler characteristic
Möbius strips having
Euler characteristic  .) Therefore
.) Therefore  , and
, and  .
.
These arguments contain more than just a proof of 2.3.A. In
particular, they imply that
3.2.C
In the case of an M-curve (i.e., if
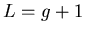
) and only in this case, the orbit space is a sphere with
holes.
Similarly, in the case of an  -curve, the orbit space is homeomorphic
to the projective plane with holes.
-curve, the orbit space is homeomorphic
to the projective plane with holes.
If 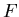 separates
separates 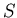 (i.e.,
(i.e.,
 is not connected), the
involution
is not connected), the
involution  is said to be of type I, otherwise it is said to
be of type II. The types correspond to the types of real
algebraic curves (see Section 2.1).
is said to be of type I, otherwise it is said to
be of type II. The types correspond to the types of real
algebraic curves (see Section 2.1).
Note that 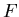 separates
separates 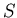 at most into two
pieces. To prove this, we can use the same arguments as in a footnote
in Section 2.1: the closure of tne union of a connected
component of
at most into two
pieces. To prove this, we can use the same arguments as in a footnote
in Section 2.1: the closure of tne union of a connected
component of
 with its image under
with its image under  is open and close in
is open and close in 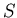 , but
, but 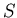 is
connected.
is
connected.
3.2.D
The orbit space
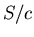
is orientable if and only if
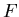
separates
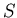
.
3.2.E (Cf.
2.6.C)
If the curve is of type I
, then
![$ L\equiv \left[\frac{m+1}2\right]\mod 2$](img500.png) .
.
Proof.
This theorem follows from
3.2.C and the calculation of
the Euler characteristic of
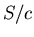
made in the proof of the Harnack
inequality above. Namely,
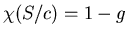
, but for any orientable
connected surface with Euler characteristic
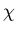
and
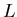
boundary components
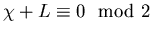
. Therefore
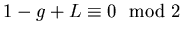
. Since
![$ g=(m-1)(m-2)/2\equiv\left[\frac{m-1}2\right] \mod2$](img505.png)
,
we obtain
![$ 1-\left[\frac{m-1}2\right]+L\equiv0\mod2$](img506.png)
which is
equivalent to the desired congruence.

Proof.
By
3.2.C, in the case of M-curve the orbit space
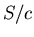
is homeomorphic to a sphere with holes. In particular, it is
orientable. By
3.2.D, this implies that
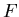
separates
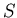
.

Now consider the simplest prohibition involving the placement
of the real part of the flexible curve in the projective plane.
3.2.G
The real part of a flexible curve is
one-sided if and only if the degree is odd.
Proof.
The proof of
3.2.G coincides
basically with the proof of the same statement for algebraic curves.
One has to consider a real projective line transversal to the flexible
curve and calculate the intersection number of the complexification of
this line and the lfexible curve. On one hand, it is equal to the degree
of the flexible curve. On the other hand, the intersection points in
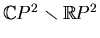
give rise to an even contribution to the intersection number.

Rokhlin's complex orientation formula also comes from topology. The
proof presented in Section 2.7 works for a flexible curve.
At this point I want to break a textbook style exposition.
Escaping a detailed exposition of prohibitions, I switch to a survey.
In the next two sections, the current state of prohibitions on
the topology of a flexible curve of a given degree is outlined.
(Recall that all formulations of this sort are automatically valid for
real projective algebraic plane curves of the same degree.)
After the survey a light outline of some proofs is proposed.
It is included just to convey a general impression, rather
than for more serious purposes. For
complete proofs, see the surveys [Wil-78], [Rok-78], [Arn-79],
[Kha-78], [Kha-86], [Vir-86] and the papers cited there.



Next: 3.3 A Survey of
Up: 3 The Topological Point
Previous: 3.1 Flexible Curves
Oleg Viro
2000-12-30


![]() -curve, the orbit space is homeomorphic
to the projective plane with holes.
-curve, the orbit space is homeomorphic
to the projective plane with holes.
![]() separates
separates ![]() (i.e.,
(i.e.,
![]() is not connected), the
involution
is not connected), the
involution ![]() is said to be of type I, otherwise it is said to
be of type II. The types correspond to the types of real
algebraic curves (see Section 2.1).
is said to be of type I, otherwise it is said to
be of type II. The types correspond to the types of real
algebraic curves (see Section 2.1).
![]() separates
separates ![]() at most into two
pieces. To prove this, we can use the same arguments as in a footnote
in Section 2.1: the closure of tne union of a connected
component of
at most into two
pieces. To prove this, we can use the same arguments as in a footnote
in Section 2.1: the closure of tne union of a connected
component of
![]() with its image under
with its image under ![]() is open and close in
is open and close in ![]() , but
, but ![]() is
connected.
is
connected.
![]() does not separate
does not separate ![]() , then one can connect a
point of
, then one can connect a
point of
![]() to its image under the involution by a path in
the complement
to its image under the involution by a path in
the complement
![]() . Such a path covers a loop in the
orbit space. This is an orientation reversing loop, since the involution
reverses orientation.
. Such a path covers a loop in the
orbit space. This is an orientation reversing loop, since the involution
reverses orientation. ![]()