


Next: 3.2 The Most Elementary
Up: 3 The Topological Point
Previous: 3 The Topological Point
3.1 Flexible Curves
In Section 1 all prohibitions were deduced from the Bézout
Theorem. In Section 2 many proofs were purely topological. A
straightforward analysis shows that the proofs of all prohibitions are
based on a small number of basic properties of the complexification of
a nonsingular plane projective algebraic curve. It is not difficult to
list all these properties of such a curve 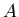 :
:
- Bézout's theorem;
-
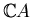 realizes the class
realizes the class
![$ m[\mathbb{C}P^1]\in H_2(\mathbb{C}P^2)$](img474.png) ;
;
-
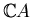 is homeomorphic to a sphere with
is homeomorphic to a sphere with
 handles;
handles;
-
 ;
;
- the tangent plane to
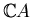 at a point
at a point
 is the
complexification of the tangent line of
is the
complexification of the tangent line of
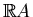 at
at  .
.
The last four are rough topological properties. Bézout's theorem
occupies a special position. If we assume that some surface
smoothly embedded into
 intersects the complex point set of
any algebraic curve as, according to Bézout's theorem, the complex
point set of an algebraic curve, then this surface is the complex point
set of an algebraic curve. Thus the Bézout theorem is completely
responsible for the whole set of properties of algebraic curves. On the
other hand, its usage in obtaining prohibitions involves a construction
of auxiliary curves, which may be very subtle.
intersects the complex point set of
any algebraic curve as, according to Bézout's theorem, the complex
point set of an algebraic curve, then this surface is the complex point
set of an algebraic curve. Thus the Bézout theorem is completely
responsible for the whole set of properties of algebraic curves. On the
other hand, its usage in obtaining prohibitions involves a construction
of auxiliary curves, which may be very subtle.
Therefore, along with algebraic curves, it is useful to consider objects
which imitate them topologically.
An oriented smooth closed connected two-dimensional submanifold 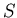 of the complex projective plane
of the complex projective plane
 is called a flexible curve
of degree
is called a flexible curve
of degree 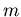 if:
if:
- (i)
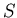 realizes
realizes
![$ m[\mathbb{C}P^1]\in H_2(\mathbb{C}P^2)$](img474.png) ;
;
- (ii)
- the genus of
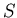 is equal to
is equal to
 ;
;
- (iii)
 ;
;
- (iv)
- the field of planes tangent to
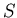 on
on
 can be
deformed in the class of planes invariant under
can be
deformed in the class of planes invariant under  into the field
of (complex) lines in
into the field
of (complex) lines in
 which are tangent to
which are tangent to
 .
.
A flexible curve 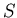 intersects
intersects
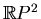 in a smooth one-dimensional
submanifold, which is called the real part of
in a smooth one-dimensional
submanifold, which is called the real part of 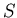 and
denoted by
and
denoted by
 . Obviously, the set of complex points of a nonsingular
algebraic
curve of degree
. Obviously, the set of complex points of a nonsingular
algebraic
curve of degree 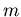 is a flexible curve of degree
is a flexible curve of degree 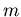 . Everything said
in Section 2.1 about algebraic curves and their (real and
complex) schemes carries over without any changes to the case of
flexible curves. We say that a prohibition on the schemes of curves of
degree
. Everything said
in Section 2.1 about algebraic curves and their (real and
complex) schemes carries over without any changes to the case of
flexible curves. We say that a prohibition on the schemes of curves of
degree 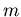 comes from topology if it can be proved for the
schemes of flexible curves of degree
comes from topology if it can be proved for the
schemes of flexible curves of degree 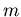 . The known classification
of schemes of degree
. The known classification
of schemes of degree  can be obtained using only the
prohibitions that come from topology. In other words, for
can be obtained using only the
prohibitions that come from topology. In other words, for  all
prohibitions come from topology.
all
prohibitions come from topology.



Next: 3.2 The Most Elementary
Up: 3 The Topological Point
Previous: 3 The Topological Point
Oleg Viro
2000-12-30
![]() of the complex projective plane
of the complex projective plane
![]() is called a flexible curve
of degree
is called a flexible curve
of degree ![]() if:
if:
![]() intersects
intersects
![]() in a smooth one-dimensional
submanifold, which is called the real part of
in a smooth one-dimensional
submanifold, which is called the real part of ![]() and
denoted by
and
denoted by
![]() . Obviously, the set of complex points of a nonsingular
algebraic
curve of degree
. Obviously, the set of complex points of a nonsingular
algebraic
curve of degree ![]() is a flexible curve of degree
is a flexible curve of degree ![]() . Everything said
in Section 2.1 about algebraic curves and their (real and
complex) schemes carries over without any changes to the case of
flexible curves. We say that a prohibition on the schemes of curves of
degree
. Everything said
in Section 2.1 about algebraic curves and their (real and
complex) schemes carries over without any changes to the case of
flexible curves. We say that a prohibition on the schemes of curves of
degree ![]() comes from topology if it can be proved for the
schemes of flexible curves of degree
comes from topology if it can be proved for the
schemes of flexible curves of degree ![]() . The known classification
of schemes of degree
. The known classification
of schemes of degree ![]() can be obtained using only the
prohibitions that come from topology. In other words, for
can be obtained using only the
prohibitions that come from topology. In other words, for ![]() all
prohibitions come from topology.
all
prohibitions come from topology.