1.3 Bézout's Prohibitions and the Harnack Inequality

The most elementary prohibitions, it seems, are the topological consequences of Bézout's theorem. In any case, these were the first prohibitions to be discovered.

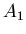
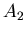
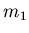
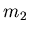
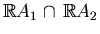
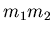
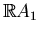
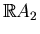
1.3.A Bézout's Theorem (see, for example, [Wal-50], [Sha-77]).   Let $A_1$ and $A_2$ be nonsingular curves of degree $m_1$ and $m_2$. If the set $\mathbb{R} A_1\cap \mathbb{R}A_2$ is finite, then this set contains at most $m_1m_2$ points. 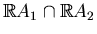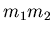If, in addition, $\mathbb{R}A_1$ and $\mathbb{R}A_2$ are transversal to one another, then the number of points in the intersection $\mathbb{R}A_1\cap \mathbb{R} A_2$ is congruent to $m_1m_2$ modulo $2$.

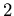
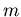
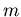
1.3.B Corollary.   A nonsingular plane curve of degree $m$ is one-sided if and only if $m$ is odd. In particular, a curve of odd degree is nonempty.

In fact, in order for a nonsingular plane curve to be two-sided, i.e., to be homologous to zero $\mod 2$, it is necessary and sufficient that its intersection number with the projective line be zero $\mod 2$. By Bézout's theorem, this is equivalent to the degree being even.$\qedsymbol$

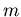
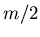
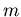
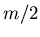
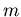
1.3.C Corollary.   The number of ovals in the union of two nests of a nonsingular plane curve of degree $m$ does not exceed $m/2$. In particular, a nest of a curve of degree $m$ has depth at most $m/2$, and if a curve of degree $m$ has a nest of depth $[m/2]$, then it does not have any ovals not in the nest.

To prove Corollary 2 it suffices to apply Bézout's theorem to the curve and to a line which passes through the insides of the smallest ovals in the nests.$\qedsymbol$

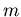
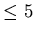
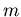
1.3.D Corollary.   There can be no more than $m$ ovals in a set of ovals which is contained in a union of $\le 5$ nests of a nonsingular plane curve of degree $m$ and which does not contain an oval enveloping all of the other ovals of the set.

To prove Corollary 3 it suffices to apply Bézout's theorem to the curve and to a conic which passes through the insides of the smallest ovals in the nests.$\qedsymbol$

One can give corollaries whose proofs use curves of higher degree than lines and conics (see Section 3.8). The most important of such results is Harnack's inequality.

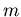
1.3.E Corollary. (Harnack Inequality [Har-76]).   The number of components of a nonsingular plane curve of degree $m$ is at most $\frac{(m-1)(m-2)}2+1$.

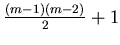
The derivation of Harnack Inequality from Bézout's theorem can be found in [Har-76], and also [Gud-74]. However, it is possible to prove Harnack Inequality without using Bézout's theorem; see, for example, [Gud-74], [Wil-78] and Section 3.2 below.