Triples of Lines

When we studied pairs of lines, an important role was played by the common perpendicular to the two skew lines. Strictly speaking, we could have avoided using it; but it seemed to be connected to the lines in such a natural way, providing a tangible tie between them, that it would have been strange not to make use of it. Now it would be good to find something equally natural for a triple of skew lines. There are two objects that are capable of playing this role. We shall discuss one of them now, and postpone consideration of the second one. Jumping ahead, suffice it to say that the second object is a hyperboloid.

These objects will not be associated to every triple of pairwise skew lines. We will have to disallow triples whose lines lie in three parallel planes. But notice that such an arrangement is unstable: by nudging one of the lines a little, we obtain an isotopic triple to which our constructions can be applied.

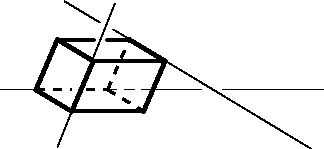
Thus, we consider an arbitrary triple of pairwise skew lines which do not lie in three parallel planes. For each line we draw two planes containing the line, each parallel to one of the other two lines. In this way we obtain six planes, i.e., three pairs of parallel planes. These planes intersect to form a parallelepiped. Our lines are the extensions of three of its skew edges (Figure 12). Thus, any three pair-wise skew lines which do not lie in three parallel planes are extensions of the edges of a certain parallelepiped. This parallelepiped is the first object which we associate to the triple of lines. What is special about it? In the first place, it is unique. In fact, there is a unique plane parallel to a given line that contains a second skew line; and if these lines are the extensions of edges of a parallelepiped, then this plane contains one of its faces. Consequently, the six planes are uniquely determined by the original triple of lines; since any parallelepiped whose edges lie on these lines is bounded by those planes, it is also uniquely determined.

Figure 12:

We see that the parallelepiped joins together the lines of the triple just as nicely as the common perpendicular joined together the lines of the pair. Just as in the case of the common perpendicular and the semi-oriented pair of nonperpendicular lines, the original geometry of the configuration naturally leads to something more, though still something which is connected with it in a canonical way and so merits our further consideration when we study the original object.

A riddle In Figure 13, despite what was proven above, we have drawn two different parallelepipeds with edges lying on three pairwise skew lines. What is going on?

Figure 13:

We now look at the classification of triples up to isotopy. As shown above, we may suppose that the lines in the triple are extensions of edges of a certain parallelepiped. A parallelepiped is determined (up to translation) by the lengths of its edges and the angles between them. Using a continuous deformation, we can first make all of the angles into right angles (obtaining a rectangular parallelepiped), and then we can make all of the edges have the same length, for example, length one (obtaining a cube) (Figure 14). This deformation induces an isotopy of the triple of lines which are extensions of edges of the parallelepiped. In this way we have managed to place the lines of our triple along pairwise skew edges of a unit cube. This is a remarkable accomplishment. It means that we now know that there are not very many possible nonisotopic sets of three skew lines--there are at most the number of triples of skew edges on a cube, and this number is 8. And even 8 is too many. We can use a rotation of the cube to take any edge of the cube to any other edge, and this reduces the number of possible nonisotopic configuration types to two. They are shown in Figure 15.

Figure 14:

Figure 15:

This success might prompt us to hope that we can similarly find an isotopy between the two triples of lines in Figure 15, and thereby prove that all triples of skew lines are isotopic. Try to do this!

You're having trouble? Don't blame yourself--it cannot be done! Just like pairs of oriented lines, triples of (nonoriented) lines have an invariant, also called the linking number, which takes the value $+1$ or $-1$, is preserved under isotopies, and changes when one takes a mirror reflection of the triple of lines. Here is its definition. Suppose we have a set of three pairwise skew lines. We orient the tree lines in an arbitrary way. Then each pair of lines in the triple has a linking number (equal to $\pm1$). If we multiply all of the linking numbers, we obtain a number (also $\pm1$), which is what we call the linking number of the original triple of lines. This number does not depend on the orientation of the lines, since if we reverse the orientation of any line, the effect is to change the linking numbers of two of the pairs, and this does not change the product. The fact that the linking number of a triple is preserved under isotopy and changes under mirror reflection follows from the corresponding properties of the linking numbers of pairs of oriented lines. Since the triples of lines in Figure 15 are the mirror images of one another, they have different linking numbers, and hence they are not isotopic to one another.

Since any triple of pairwise skew lines is isotopic to one of the two triples in Figure 15, it follows that two triples of lines are isotopic if and only if they have the same linking number.

Thus, as soon as we reach three lines we find that there are different possible arrangements of triples of skew lines. This provides a justification for the title of the paper, and for our subsequent use of the word interlacing for a set of pairwise skew lines.

Problem. It is natural to expect that the linking number of a triple of nonoriented lines is equal to the linking number of some pair of semi-oriented lines which can be constructed from the triple in a canonical way. This is in fact the case, except that rather than one such semi-oriented pair there are three. Prove that for any triple of skew lines there is a unique semi-orientation such that the linking numbers of all three pairs of lines in the triple are equal. Obviously, this value is also equal to the linking number of the triple.