Four Lines

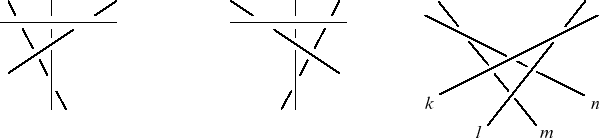
At this point we have actually already encountered all of the types of interlacings of four lines. There are three of them, and they are depicted in Figure 23. The interlacing in Figure 16 is on the left, its mirror image is in the center, and the interlacing in Figure 17 is on the right. We have already proved that these three sets are not isotopic to one another: the first one is not amphicheiral, and so is not isotopic to the second one, and the third one is amphicheiral, and so is not isotopic to either the first or the second.

Figure 23: Interlacings of 4 lines.

In order to show that any interlacing of four lines is isotopic to one of the interlacings in Figure 23, we shall have to make use of the second of the two objects which, as mentioned above, are associated to a triple of lines. This is a one-sheeted hyperboloid--a surface which is usually studied in analytic geometry. There one learns that a one-sheeted hyperboloid (henceforth referred to simply as a hyperboloid) is made up of lines--its generatrices. Any two generatrices in the same family are skew, while any two generatrices in different families are either parallel or intersect. We list some other properties of hyperboloids which we shall need:

(1) if a line has three points in common with a hyperboloid, then it is a generatrix;

(2) a plane containing a generatrix of a hyperboloid intersects the hyperboloid in two generatrices;

(3) there is a hyperboloid passing through any three pairwise skew lines which do not lie in parallel planes.

These properties are simple consequences of the fact that a hyperboloid is a surface of degree two. Of course, one could describe all of this without appealing to analytic geometry, using the same language as the ancient Greeks, but we shall not try the reader's patience by proceeding in that way.

Thus, in order to complete the isotopy classification of four-tuples of lines, we shall prove that any interlacing of four lines is isotopic to one of the interlacings in Figure 23. We take an arbitrary interlacing of four lines. By moving it slightly, if necessary, we can obtain a situation where three of the four lines (it makes no difference which three) do not lie in parallel planes. We construct a hyperboloid through these three lines, and we observe how the fourth line is situated relative to the hyperboloid. There are four possibilities:

(a) the line does not intersect the hyperboloid;

(b) the line intersects the hyperboloid in a single point;

(c) the line intersects the hyperboloid in two points;

(d) the line lies on the hyperboloid.

In case (d) the interlacing of four lines consists of four generatrices of the hyperboloid, and is obviously isotopic to the left or the center interlacing in Figure 23.

If the fourth line does not intersect the hyperboloid, then it can be brought in toward the hyperboloid until it is tangent to the hyperboloid, i.e., the first case can easily be reduced to case (b).

Figure 24:

Case (b), in turn, reduces to either (c) or (d). To see this, we draw a generatrix $l$ through the point of intersection of the hyperboloid with the fourth line, where $l$ is taken in the same family of generatrices as the first three lines of the interlacing. By property (3), the plane $a$ containing $l$ and the fourth line intersects the hyperboloid in two generatrices $l$ and $l'$. If $l'$ intersects $l$ and the fourth line in the same point, then, rotating the fourth line around this point of intersection in the plane $a$ until it coincides with $l$, we find ourselves in case (d) (Figure 24(a)). Otherwise, the fourth line of the interlacing is parallel to $l'$ (if this weren't the case we would have case (c)) (see Figure 24(b)). But if we perform a small rotation toward the fourth line around the intersection point with $l$ in the plane $a$, we see that the fourth line is no longer parallel to $l'$: it intersects $l'$, and hence it intersects the hyperboloid in two points, giving us case (c).

Now if the fourth line intersects the hyperboloid in two pints, then everything depends on whether these points are in the same part of the hyperboloid into which the first three lines divide it, or are in different parts (the hyperboloid is divided into three sections). If they are in the same part, then the fourth line can be placed on the hyperboloid without the first three lines interfering. Then the fourth line becomes a generatrix, and we are in case (d). If the fourth line intersects the hyperboloid in different parts, then the interlacing is isotopic to the right interlacing in Figure 23.