2.4 Further Examples

Next: 2.5 Digression: Oriented Topological Up: 2 A Real Algebraic Previous: 2.3 Classical Small Perturbations

2.4 Further Examples

Although Theorem 2.3.A describes only a very special class of classical small perturbations (namely perturbations of unions of nonsingular curves intersecting only in real points), it is enough for all constructions considered in Section 1. In Figures 17, 18, 19, 20, 21, 22 and 23 I reproduce the constructions of Figures 2, 3, 4, 6, 7, 10 and 11, enhancing them with complex orientations if the curve is of type I.

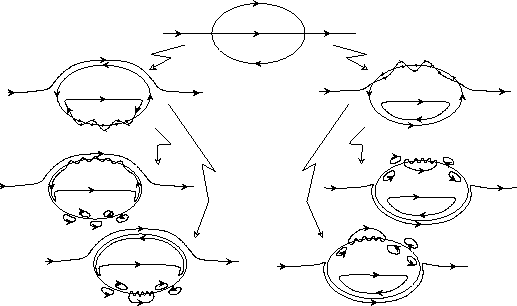
**Figure 20:** Construction of a quintic M-curve with its complex orientation. Cf. Figure 6.
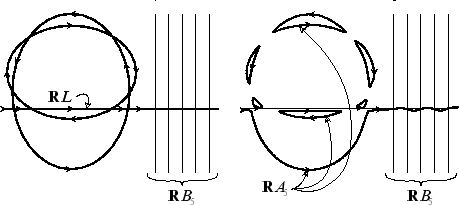$\begin{figure}\centerline{\epsffile{f6-1s.eps}}\end{figure}$

**Figure 21:** Harnack's construction with complex orientations. Cf. Figure 7.
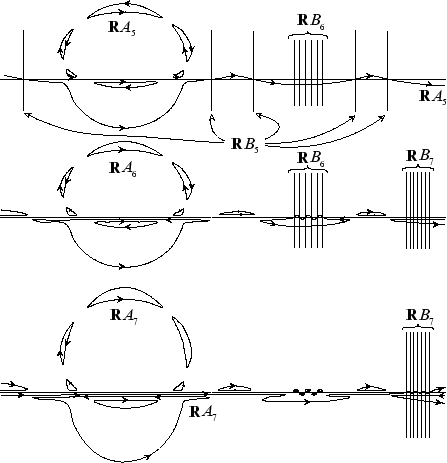$\begin{figure}\centerline{\epsffile{f7-1s.eps}}\end{figure}$

**Figure 22:** Construction of even degree curves by Hilbert's method. Degrees 4 and 6. Cf. Figure 10.
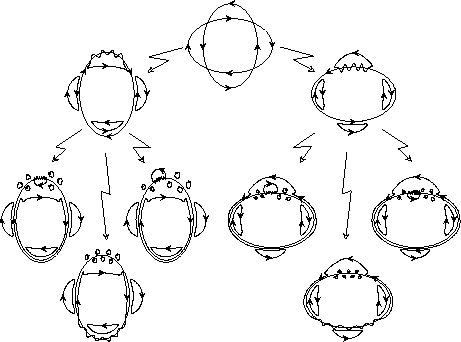$\begin{figure}\centerline{\epsffile{f10-1s.eps}}\end{figure}$

**Figure 23:** Construction of odd degree curves by Hilbert's method. Degrees 3 and 5. Cf. Figure 11.
$\begin{figure}\centerline{\epsffile{f11-1s.eps}}\end{figure}$

Next: 2.5 Digression: Oriented Topological Up: 2 A Real Algebraic Previous: 2.3 Classical Small Perturbations

Oleg Viro 2000-12-30