Biography |
Михаил Шлемович Бирман
2 июля 2009 г. ушел из жизни Михаил Шлемович Бирман — выдающийся математик, один из мировых лидеров в спектральной теории операторов.
Михаил Шлемович Бирман родился 17 января 1928 г. в Ленинграде. Его отец был ученым — специалистом по теоретической механике, профессором. Мать была школьной учительницей.
М. Ш. Бирман учился на математико-механическом факультете Ленинградского государственного университета в 1946–1950 гг. Специализировался по методам вычислений. Своими учителями Михаил Шлемович считал Марка Константиновича Гавурина, который был руководителем его дипломной работы, и Леонида Витальевича Канторовича. Еще будучи студентом, М. Ш. подрабатывал в Ленинградском отделении математического института в лаборатории Канторовича. Он был лучшим студентом на курсе, с высоким интеллектом и независимым мышлением. Но в аспирантуру его не взяли из-за тогдашней политики антисемитизма.
В 1947 г. Михаил Шлемович женился на своей сокурснице Татьяне Петровне Ильиной. В 1948 г. у них родился сын Женя. С Татьяной Петровной они счастливо прожили всю жизнь. Она ушла из жизни двумя годами раньше него. Она всегда была его добрым ангелом-хранителем. Благодаря ее заботе и любви он мог полностью посвятить себя своему любимому делу — занятиям математикой.
После окончания университета М. Ш. работал в Ленинградском горном институте на кафедре высшей математики ассистентом. В 1954 году успешно защитил кандидатскую диссертацию.
Большую роль в научном становлении Михаила Шлемовича сыграло его активное участие в работе Ленинградского семинара по математической физике, организованного в начале 50-х годов по инициативе Владимира Ивановича Смирнова. Впоследствии в течение многих лет М. Ш. вместе с Ольгой Александровной Ладыженской руководил этим семинаром.
По предложению Владимира Ивановича и Ольги Александровны, в 1956 году Михаил Шлемович перешел работать в ЛГУ, на кафедру математической физики физического факультета. На кафедре математической физики М. Ш. проработал до конца своей жизни — более 50-ти лет. В 1962 г. он защитил докторскую диссертацию на тему "Спектр сингулярных граничных задач". М. Ш. был блестящим лектором. Он был одним из лидеров кафедры, и не только научным. Он не только обладал высочайшим профессиональным авторитетом, но всегда был очень внимателен к людям. Многие его младшие коллеги испытывали его влияние, как прекрасного профессионала и мудрого человека. У него всегда были очень высокие профессиональные стандарты — как к качеству результатов, так и к изложению материала. И прежде всего эти требования он предъявлял самому себе.
Михаил Шлемович вместе со своим соратником Михаилом Захаровичем Соломяком создал сильную научную школу по спектральной теории операторов, известную во всем мире. Многие его ученики сами стали известными учеными и работают сейчас в ведущих университетах России и на Западе.
Михаил Шлемович Бирман — автор более 160 научных статей и двух книг. Он много занимался редакторской деятельностью, был членом редколлегий журналов РАН "Алгебра и анализ", "Функциональный анализ и его приложения". Заслуги М. Ш. Бирмана были отмечены почетными званиями "Заслуженный деятель науки РФ", "Почетный профессор СПбГУ". В 2008 г. он получил награду правительства Санкт-Петербурга и Санкт-Петербургского центра РАН — медаль и премию имени П. Л. Чебышева за заслуги в области математики.
Работы М. Ш. Бирмана получили международное признание и обильно цитируются в математической литературе. Он многократно был пленарным докладчиком на международных конференциях. Его приглашали с научными визитами в ведущие университеты и научные центры мира.
Остановимся кратко на главных научных достижениях М. Ш. Бирмана.
Ранние работы (1950–1952).
Первые работы М. Ш. Бирмана выполнены под влиянием Канторовича и Гавурина. Они посвящены вычислительным вопросам в задачах линейной алгебры, а именно, многошаговому итерационному методу наискорейшего спуска. Разработанные им методы были внедрены в практику расчетов.Теория расширений. Эллиптические граничные задачи (1953–1962).
Следующий важный цикл работ Михаила Шлемовича относится к теории расширений симметричных положительно определенных операторов и применению этой теории к эллиптическим граничным задачам. Он пришел к этой тематике, занимаясь вычислительными методами, связанными с вариационным подходом к решению граничных задач. Осознав роль общей теории расширений в этом круге вопросов, он стал изучать работы Марка Григорьевича Крейна и Марка Иосифовича Вишика по этой теории. Особенно большое впечатление на него произвели работы Крейна, которые, по словам М. Ш., открыли для него новый мир. С тех пор М. Ш. всегда считал себя "заочным учеником" М. Г. Крейна.Развивая идеи Крейна и Вишика, М. Ш. построил параметрическое описание всех самосопряженных расширений данного симметричного положительно определенного оператора. Этот подход был успешно применен в работах по вариационным методам.
Вместе с тем, М. Ш. обнаружил и другие, еще более важные приложения своих результатов по теории расширений. Речь идет об устойчивости существенного спектра для эллиптических операторов в неограниченных областях. Именно, М. Ш. установил, что существенный спектр устойчив относительно изменения компактной части границы или граничных условий на такой части границы. Были получены оценки собственных значений для разности резольвент одного и того же эллиптического оператора с различными граничными условиями.
В знаменитой работе М. Ш. Бирмана "О спектре сингулярных граничных задач" (Мат. сб., 1961) изучалась устойчивость существенного спектра при изменении коэффициентов оператора. Типичный пример — сравнение спектров оператора H0 = -Δ и оператора Шредингера H = -Δ + V, действующих в L2(Rd). Здесь V(x)→0 при |x|→∞. Результаты этой работы дают новый взгляд и на общую теорию возмущений. Основной прием, который можно назвать "фирменным знаком" М. Ш., состоит в последовательном применении квадратичных форм. Явного описания "действия" оператора, а также его области определения, при этом удается избежать. В частности, М. Ш. широко использует понятие, позднее названное "относительной компактностью в смысле квадратичных форм".
Перечислим некоторые результаты, полученные в статье. Для полуограниченного снизу самосопряженного оператора A существенный спектр устойчив при возмущениях относительно компактным оператором (в смысле квадратичных форм). Пусть V — такой оператор. Тогда существенные спектры операторов A и A+V совпадают.
Пусть в прежних условиях V ≥ 0 и рассматривается оператор A+ α V, &alpha < 0. Тогда спектр оператора A + α V, лежащий левее спектра A, дискретен. М. Ш. нашел соотношение, связывающее функцию распределения дискретного спектра оператора A + α V c функцией распределения собственных значений компактного оператора, порожденного формой оператора V в энергетическом пространстве оператора A. Это соотношение двумя годами позже было переоткрыто Швингером и носит название принципа Бирмана-Швингера.
Сейчас принцип Бирмана-Швингера — исходная точка при изучении дискретного спектра операторов с непустым существенным спектром. Особенно часто он применяется в задачах квантовой механики.
Общие результаты статьи были применены к дифференциальным операторам. В частности, для оператора Шредингера H = -Δ - V(x) в L2(R3) была получена знаменитая оценка Бирмана-Швингера числа отрицательных собственных значений
 \le {1 \over 16 \pi^2} \int_{{\mathbf R}^3}\int_{{\mathbf R}^3}{V_+({\mathbf x}) V_+({\mathbf y})\,d{\mathbf x}\, d{\mathbf y} \over |{\mathbf x}-{\mathbf y}|^2}. )
Математическая теория рассеяния (60-е годы).
Особо нужно выделить работы Михаила Шлемовича по математической теории рассеяния. Его работы оказали значительное влияние на становление и развитие этой области.Поясним основные идеи теории рассеяния. В работах Т. Като и
М. Розенблюма был установлен следующий фундаментальный факт. Пусть
A и B — самосопряженные операторы в гильбертовом
пространстве H, Pac(A) — ортопроектор на
абсолютно непрерывное подпространство Hac(A)
оператора A. Предположим, что A-B ∈  , где
, где
 — класс ядерных операторов. Тогда существуют сильные
пределы
— класс ядерных операторов. Тогда существуют сильные
пределы
 = W_\pm(B,A) ) (1)
(1)
называемые волновыми операторами. Операторы W± изометричны на Hac(A) и B W± = W± A. Отсюда выводится, что абсолютно непрерывные части операторов A и B унитарно эквивалентны.
Оператор рассеяния
S = W+* W-
коммутирует с A. Если представить пространство Hac(A) в виде прямого интеграла
\,d\lambda ) , в котором диагонализуется оператор
Aac, то
S действует как умножение на оператор-функцию S(λ), называемую матрицей рассеяния.
, в котором диагонализуется оператор
Aac, то
S действует как умножение на оператор-функцию S(λ), называемую матрицей рассеяния.
Для приложений к квантовой механике важный случай представляет рассеяние для оператора Шредингера. Тогда A=-Δ и B = -Δ + V(x), где V(x) — вещественный потенциал, причем V(x) стремится к нулю достаточно быстро при |x|→ ∞. Теорема Розенблюма-Като не может быть прямо применена к этому случаю, поскольку оператор умножения на V(x) в L2(Rd) не является компактным.
Вклад М. Ш. в решение этой проблемы был решающим. Его идея состояла в том, чтобы рассмотреть подходящие функции φ от операторов A и B и применить теорему Розенблюма-Като к операторам φ(A), φ(B). Он показал, что при условии ядерности оператора φ(A) - φ(B) не только совпадают абсолютно непрерывные спектры операторов A и B, но и существуют волновые операторы W±(B, A) и
W±(B,A) = W±(φ(B), φ(A)).
Этот результат, доказанный Михаилом Шлемовичем для широкого класса функций 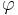 ,
был позднее назван принципом инвариантности.
,
был позднее назван принципом инвариантности.
Важный вклад в теорию рассеяния был сделан в работах М. Ш., совместных с Марком Григорьевичем Крейном. Они распространили теорему Розенблюма-Като на случай унитарных операторов. Это соответствует принципу инвариантности для дробно-линейной функции φ. Теорема Бирмана-Крейна показывает, что для пары самосопряженных операторов A,B волновые операторы W±(B,A) существуют, если разность резольвент ядерная. Этот результат уже непосредственно применим к оператору Шредингера.
М. Ш. ввел важное понятие локальных волновых операторов, связанных с каким-либо интервалом спектральной оси. С их помощью он нашел очень общие условия существования "глобальных" волновых операторов.
Наряду с зависящей от времени формулировкой теория рассеяния допускает стационарную формулировку. При этом вместо пределов (1) при t → ± ∞ приходится изучать пределы резольвент при стремлении спектрального параметра к вещественной оси. Этот подход позволяет дать формульные представления для основных объектов теории, что важно для физических приложений. Совместно с С. Б. Энтиной, М. Ш. последовательно развил стационарную схему в ядерной теории рассеяния, получив при этом важные результаты о предельных значениях резольвент. Позднее М. Ш. вернулся к этой тематике, развив совместно с Д. Р. Яфаевым общую стационарную схему вне рамок конкретных предположений ядерного или гладкого типов.
Функция спектрального сдвига.
С теорией рассеяния тесно связаны исследования функции спектрального сдвига. Для пары самосопряженных операторов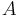 ,
, 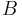 при определенных условиях
имеет место формула следов:
при определенных условиях
имеет место формула следов:
 - \varphi(A)) = \int_{-\infty}^\infty \varphi' (\lambda) \xi(\lambda)\,d\lambda. ) (2)
(2)
Функцию ξ(λ) называют функцией спектрального сдвига (ФСС). Понятие ФСС в теории возмущений было введено в начале 50-х годов физиком И. М. Лифшицем. Вскоре после этого М. Г. Крейн развил математическую теорию ФСС. Он оправдал формулу (2) для самосопряженных операторов A, B с ядерной разностью и для широкого класса функций φ.
Совместно М. Ш. и М. Г. Крейн в 1962 г. установили знаменитую формулу Бирмана-Крейна — связь
между функцией спектрального сдвига и матрицей рассеяния. Они показали, что при
A-B ∈  разность S(λ) -I ядерна при
п. в. λ ∈ σac(A).
Тогда детерминант S(λ) корректно определен и справедлива формула
разность S(λ) -I ядерна при
п. в. λ ∈ σac(A).
Тогда детерминант S(λ) корректно определен и справедлива формула
 = \exp (-2\pi i \xi(\lambda)). )
Работа Бирмана и Крейна явилась основой для дальнейших исследований многими авторами (включая самого М. Ш.) свойств ξ(λ) и S(λ).
Двойные операторные интегралы (1965–1973).
В 1965 г. началась совместная работа М. Ш. Бирмана с М. З. Соломяком. Первый большой и важный цикл их совместных работ посвящен систематическому изучению ДОИ (двойных операторных интегралов). М. Ш. заинтересовался ДОИ потому, что в теории рассеяния возникла техническая потребность в этом аппарате. В дальнейшем выяснилось, что ДОИ имеют приложения в самых разных областях.Двойной операторный интеграл — это выражение вида
\,dF(\mu)\, T \, dE(\lambda), )
где dE(λ), dF(μ) — спектральные меры в гильбертовом пространстве,
T — ограниченный оператор, ψ — некоторая скалярная функция переменных λ, μ.
При фиксированных ψ, dF, dE получаем отображение Ψ:T→Q.
ДОИ были введены в работе Ю. Л. Далецкого и С. Г. Крейна в 1956 г.
В серии совместных работ М. Ш. Бирман и М. З. Соломяк построили строгую теорию ДОИ, как
преобразований в классах Шаттена - фон Неймана  .
.
Одно из важных приложений ДОИ относится к теории возмущений. Если A и B — самосопряженные операторы, и dE, dF — их спектральные меры, то
 - \varphi(A) = \int \int {\varphi(\lambda) - \varphi(\mu) \over \lambda - \mu}\, dE(\lambda) \,(B-A)\,dF(\mu). )
Эта формула была оправдана М. Ш. Бирманом и М. З. Соломяком для широкого класса функций φ.
Метод кусочно-полиномиальных приближений и его применения (60-е, 70-е годы).
Совместно с М. З. Соломяком, М. Ш. Бирман предложил новый подход к аппроксимации функций из классов Соболева ) .
.
Хотя непосредственным поводом для этого послужили нужды теории ДОИ, основные применения лежат далеко за
ее рамками. Наиболее яркий результат, полученный на основе этого метода (в 1967 г.), — это
точные по порядку оценки ε-энтропии вложения пространств Соболева
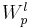 в C или в Lq в случаях, когда такое вложение компактно.
Именно, было показано, что порядок оценки зависит только от гладкости l, но не от показателя p.
в C или в Lq в случаях, когда такое вложение компактно.
Именно, было показано, что порядок оценки зависит только от гладкости l, но не от показателя p.
Еще одно приложение — оценки и асимптотики спектра для широкого класса интегральных операторов (статья 1977 г. в УМН).
Результаты по кусочно-полиномиальным приближениям оказались также чрезвычайно полезными при доказательстве оценок и асимптотических формул для дискретного спектра дифференциальных операторов. Для примера рассмотрим граничную задачу с весовой функцией V:
 u,\ \ u\vert_{\partial \Omega} =0. ) (3)
(3)
Пусть N±(λ) — функция распределения положительных и отрицательных собственных значений задачи. При достаточно "хороших" ∂ Ω и V была известна асимптотическая формула Вейля
 \sim \lambda^{d/2} c_0(d) \int_\Omega V_\pm^{d/2}\,d{\mathbf x}, \ \ \lambda \to \infty;\ \ c_0(d)^{-1} = \Gamma(d/2 +1) 2^d \pi^{d/2}. ) (4)
(4)
На основе кусочно-полиномиальных приближений М. Ш. Бирман и М. З. Соломяк разработали новый вариант вариационного подхода, который позволил доказывать спектральные асимптотики без каких-либо предположений о гладкости данных задачи. Перечислим некоторые результаты, полученные на этом пути.
1) Вейлевская асимптотика (4) для задачи (3) справедлива в любой ограниченной области Ω, если V ∈ L1(Ω) при d=1, V ∈ Lp(Ω), p > d/2, при d ≥ 2.
Впоследствии при d ≥ 3 формула (4) была оправдана при V ∈ Ld/2(Ω) Г. В. Розенблюмом.
2) Вейлевская асимптотика спектра в задаче Дирихле была оправдана для произвольных эллиптических операторов второго порядка, заданных в дивергентной форме, без каких-либо предположений о гладкости коэффициентов и границы (в задаче Неймана — в случае липшицевой границы). Были найдены и асимптотические формулы для более общих задач, включая случай эллиптических систем.
3) Получена асимптотика спектра для ПДО отрицательного порядка.
4) Исследованы спектральные оценки и асимптотики для вариационных задач со связями.
Оператор Максвелла в негладких областях.
У М. Ш. всегда был интерес к изучению операторов математической физики в негладких областях и с негладкими коэффициентами. В частности, он считал важным исследовать эти вопросы для оператора Максвелла. Основная трудность здесь в том, что оператор неполуограничен и поэтому нельзя использовать подход через квадратичные формы. В связи с этим свойства решений не допускают описания в терминах стандартных пространств Соболева. Другая трудность — необходимость учета условий соленоидальности.М. Ш. атаковал различные задачи, связанные с оператором Максвелла, на протяжении многих лет. В работах, совместных с М. З. Соломяком (1987 г.), было дано исчерпывающее описание особенностей электрической компоненты электромагнитного поля в областях с липшицевой границей. Базируясь на этом результате, авторы оправдали вейлевскую асимптотику частот электромагнитных колебаний для ограниченных областей с липшицевыми границами. Окончательный результат в этом направлении получен совсем недавно — в 2007 г. М. Ш. Бирман совместно со своим учеником Н. Д. Филоновым доказал вейлевскую асимптотику спектра для оператора Максвелла в общем случае — в области с липшицевой границей при негладких коэффициентах.
Оценки и асимптотики отрицательного дискретного спектра оператора Шредингера и спектра в лакунах (1988–2004).
Рассмотрим оператор - Δ - α V в L2(Rd), где потенциал V(x) → 0 при |x| → ∞; α > 0 — константа связи. Пусть N-(-Δ - α V) — количество отрицательных собственных значений этого оператора. Если V ∈ Ld/2(Rd), d ≥ 3, то справедлива вейлевская асимптотика \sim c_0(d) \alpha^{d/2} \int_{{{\mathbf R}}^d} V_+^{d/2}\,dx,\ \ \alpha \to \infty. ) (5)
(5)
Назовем этот случай "регулярным".
Может быть и нерегулярный случай, когда потенциал убывает медленно и не принадлежит классу Ld/2(Rd), но число отрицательных собственных значений оператора -Δ - α V конечно. Эффекты, возникающие в нерегулярном случае, были подробно исследованы М. Ш. совместно с М. З. Соломяком. Были получены соответствующие оценки и асимптотики. Выяснилось, что для любого заданного q > d/2 можно указать класс потенциалов V, для которых N-(-Δ - α V) = O(αq). В двумерном случае (исследованном М. Ш. совместно с А. А. Лаптевым) обнаружился интересный эффект — был найден класс потенциалов, для которых асимптотика N-(-Δ - α V) имеет вейлевский порядок O(λ), а асимптотический коэффициент есть сумма вейлевского и "порогового" членов.
Аналогичные эффекты были изучены и для дискретного спектра оператора Дирака и периодического оператора Шредингера, возникающего во внутренних спектральных лакунах при возмущении убывающим потенциалом.
Проблема абсолютной непрерывности спектра периодических дифференциальных операторов (1997–2004).
В последние 10-12 лет своей жизни М. Ш. Бирман основное внимание уделял спектральной теории периодических дифференциальных операторов. Здесь нужно выделить серию работ (совместных с Т. А. Суслиной) по проблеме абсолютной непрерывности спектра периодических операторов математической физики.Спектр периодического эллиптического оператора имеет зонную структуру — он состоит из замкнутых отрезков вещественной оси (спектральных зон). Если какая-то из зон вырождается в точку, то такая точка является собственным значением бесконечной кратности. Если таких вырожденных зон нет, то спектр оператора оказывается чисто абсолютно непрерывным.
Впервые отсутствие вырожденных зон для периодического оператора Шредингера H = -Δ + V(x) в L2(Rd) было доказано Л. Томасом в 1973 г. Оператор H раскладывается в прямой интеграл по операторам H(k), действующим в L2(Ω) (где Ω — ячейка решетки периодов). Здесь H(k) = (D+k)2 +V(x) с периодическими граничными условиями. Томас предложил подход, связанный с аналитическим продолжением оператора H(k) по квазиимпульсу k и оценкой обратного оператора H(k)-1 при большой мнимой части k. При этом удавалось сначала получить нужные оценки для свободного оператора (при V=0), а затем учесть V как аддитивное возмущение.
Дальнейшие попытки обобщить результат Томаса на случай периодического магнитного оператора Шредингера терпели провал. После почти 25-летнего застоя в работе М. Ш. Бирмана и Т. А. Суслиной в 1997 г. была установлена абсолютная непрерывность спектра магнитного периодического оператора Шредингера M = (D - A(x))2 + V(x) в размерности d=2. Главная трудность в применении схемы Томаса была в том, что магнитный член — оператор первого порядка, и его не удается учесть аддитивно. Подход авторов был основан на анализе двумерного оператора Паули, который допускает удобную факторизацию. За счет этого удается учесть магнитный потенциал как мультипликативное возмущение. Эта работа сыграла роль прорыва в данной области.
Новый спектральный подход к гомогенизации периодических дифференциальных операторов (2000–2009).
Последний большой цикл работ М. Ш. Бирмана (совместный с Т. А. Суслиной) состоит в разработке нового теоретико-операторного подхода к теории усреднений (гомогенизации) периодических дифференциальных операторов.Поясним суть дела. Пусть A = -div g(x) ∇ — оператор в L2(Rd), где матрица g(x) — ограниченная, положительно определенная и периодическая относительно некоторой решетки. Рассмотрим оператор Aε=-div g(x/ε)∇, ε > 0, коэффициенты которого быстро осциллируют при малом ε. Типичная задача теории усреднений состоит в изучении поведения решения uε уравнения Aε uε + uε = F, F ∈ L2(Rd). Было известно, что при ε → 0 решение uε сходится (в некотором смысле) к решению u0 "усредненного" уравнения A0u0+u0=F. Здесь A0 = -divg0 ∇ — эффективный оператор, а g0 — постоянная положительная эффективная матрица.
С помощью нового подхода впервые удалось доказать, что резольвента оператора Aε сходится к резольвенте эффективного оператора по операторной норме в L2. Более того, имеет место оценка
^{-1} - (A^0+I)^{-1}\|_{L_2 \to L_2} \le C \varepsilon. ) (6)
(6)
Основная идея предлагаемого подхода состоит в том, что процесс усреднения можно изучать как спектральный пороговый эффект на краю спектра оператора A. С помощью масштабного преобразования оценка (6) сводится к неравенству
^{-1} - (A^0+ \varepsilon^2 I)^{-1}\|_{L_2 \to L_2} \le C \varepsilon^{-1}, ) (7)
(7)
которое удается доказать, описывая поведение резольвенты (A + ε2 I)-1 в терминах пороговых характеристик оператора A на краю спектра.
Подобные "операторные оценки погрешности", а также более точные аппроксимации резольвенты, были получены для широкого класса матричных дифференциальных операторов. На основе разработанного метода изучалась гомогенизация в параболических задачах, для стационарной системы Максвелла, и наконец, для нестационарных уравнений типа Шредингера и гиперболического типа.
Несмотря на плохое состояние здоровья, Михаил Шлемович сохранял творческую активность до последних дней своей жизни. Он жил в науке и в профессии до конца. Память о Михаиле Шлемовиче Бирмане навсегда сохранится в сердцах тех, кому посчастливилось знать этого замечательного ученого и человека.