- ... disjoint.1
- This is explained by the fact that, in the space of all
configurations of
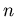 disjoint lines in
disjoint lines in
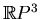 , the configurations containing a line in the
plane at infinity form a subset of codimension 2.
, the configurations containing a line in the
plane at infinity form a subset of codimension 2.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... space.2
- Here are two other problems which are also equivalent: the
problem of
classifying sets of pairwise transversal two-dimensional subspaces in
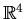 ,
with respect to motions under which they remain pairwise transversal
two-dimensional subspaces; and the problem of classifying links in the sphere
,
with respect to motions under which they remain pairwise transversal
two-dimensional subspaces; and the problem of classifying links in the sphere
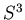 which are made up of great circles on the sphere, with respect to
isotopies under which the circles remain disjoint great circles on
which are made up of great circles on the sphere, with respect to
isotopies under which the circles remain disjoint great circles on 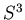 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... configurations.3
- We have already encountered this construction. The
isotopy join
interlacings introduced above (when we treated interlacings of six lines) are
essentially the joins of sets of points on a line.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.