


Next: 1.9 Isotopy Types of
Up: 1 Early Study of
Previous: 1.7 Digression: the Space
1.8 End of the Proof of Theorem 1.6.A
In Section 1.6 it was shown that for any 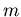 there
exist nonsingular curves of degree
there
exist nonsingular curves of degree 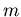 with the minimum number
with the minimum number
 or with the maximum number
or with the maximum number
 of
components. Nonsingular curves which are isotopic to one another form
an open set in the space
of
components. Nonsingular curves which are isotopic to one another form
an open set in the space
 of real projective plane curves of
degree
of real projective plane curves of
degree 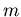 (see Section 1.7). Hence, there exists a real pencil
of curves of degree
(see Section 1.7). Hence, there exists a real pencil
of curves of degree 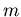 which connects a curve with minimum number of
components to a curve with maximum number of components and which
intersects the set of real
singular curves only in its principal part and only transversally. As we move
along this pencil from the curve with minimum number of components to the curve
with maximum number of components, the curve only undergoes Morse
modifications, each of which changes the number of components by at most 1.
Consequently, this pencil includes nonsingular curves with an arbitrary
intermediate number of components.
which connects a curve with minimum number of
components to a curve with maximum number of components and which
intersects the set of real
singular curves only in its principal part and only transversally. As we move
along this pencil from the curve with minimum number of components to the curve
with maximum number of components, the curve only undergoes Morse
modifications, each of which changes the number of components by at most 1.
Consequently, this pencil includes nonsingular curves with an arbitrary
intermediate number of components.



Next: 1.9 Isotopy Types of
Up: 1 Early Study of
Previous: 1.7 Digression: the Space
Oleg Viro
2000-12-30