


Next: About this document ...
Up: Configurations of Skew Lines
Previous: Connection with Real Algebraic
-
- 1
- O. Ya. Viro, Yu. V. Drobotukhina Spleteniia
skrescivaiuscikhsia priamykh, Kvant, 1988, no. 3.
- 2
- O. Ya. Viro, Yu. V. Drobotukhina Configurations of
skew lines, Algebra i analiz 1:4 (1989), (Russian)
(Russian) English transl., Leningrad Math. J. 1:4 (1990),
1027-1050.
- 3
- O. Ya. Viro, Topological problems concerning lines
and points of three-dimensional space Soviet Math. Dokl.
32:2 (1985), 528-531.
- 4
- V. F. Mazurovski
 ,
Configurations of six skew lines Zap. Nauchn. Sem.
Leningrad. Otdel. Mat. Inst. Steklov. (LOMI) 167
(1988), 121-134.
,
Configurations of six skew lines Zap. Nauchn. Sem.
Leningrad. Otdel. Mat. Inst. Steklov. (LOMI) 167
(1988), 121-134.
- 5
-
V. F. Mazurovski
 , Configurations of at most six lines of
, Configurations of at most six lines of
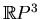 , Real Algebraic Geometry, Proceedings of the conference held in
Rennes, France, June 24-28, 1991, Lecture Notes in Math., vol 1524,
1992, 354-371.
, Real Algebraic Geometry, Proceedings of the conference held in
Rennes, France, June 24-28, 1991, Lecture Notes in Math., vol 1524,
1992, 354-371.
- 6
-
V. F. Mazurovski
 , Kauffman polynomials for nonsingular
configurations of projective lines,
Uspekhi Mat. Nauk 44:5 (1989), 173-174; English transl., Russian
Math. Surveys 44 (1989), no. 5, 212-213.
, Kauffman polynomials for nonsingular
configurations of projective lines,
Uspekhi Mat. Nauk 44:5 (1989), 173-174; English transl., Russian
Math. Surveys 44 (1989), no. 5, 212-213.
- 7
-
J.V.Drobotukhina, An analogue of the Jones polynomial for links in
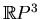 and a generalization of the Kauffman-Murasugi theorem
Algebra i analiz
2:3 (1990) (Russian) English transl.,
Leningrad Math. J. 2:3 (1991), 613-630.
and a generalization of the Kauffman-Murasugi theorem
Algebra i analiz
2:3 (1990) (Russian) English transl.,
Leningrad Math. J. 2:3 (1991), 613-630.
- 8
- Alberto Borobia and Vladimir F. Mazurovski
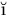 , Nonsingular configurations of 7 lines of
, Nonsingular configurations of 7 lines of
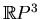 Preprint
U.U.D.M. Report 1995:41, Department of Mathematics, Uppsala
University.
Preprint
U.U.D.M. Report 1995:41, Department of Mathematics, Uppsala
University.
- 9
- V. F. Mazurovski
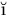 , N. B. Pavlov, Classification of
ordered nonsingular configurations of
, N. B. Pavlov, Classification of
ordered nonsingular configurations of 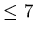 lines of
lines of
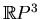 up to
rigid isotopy, Issledovaniya po topologii. 8 (Zapiski Nauchnykh
Seminarov POMI, vol. 231), SPb, (1995) 269-285 (Russian).
up to
rigid isotopy, Issledovaniya po topologii. 8 (Zapiski Nauchnykh
Seminarov POMI, vol. 231), SPb, (1995) 269-285 (Russian).
- 10
- S. S. Podkorytov, Amphicheiral configurations of
points and lines and algebraic surfaces of degree 4, Issledovaniya po
topologii. 8 (Zapiski Nauchnykh Seminarov POMI, vol. 231), SPb,
(1995) 286-298 (Russian).
- 11
- S. M. Finashin,
Configurations of seven points in
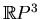 ,
Topology and Geometry (Rokhlin Seminar), Lecture Notes in Math.,
vol. 1346,
Springer (1988), 501-526.
,
Topology and Geometry (Rokhlin Seminar), Lecture Notes in Math.,
vol. 1346,
Springer (1988), 501-526.
- 12
- N. E. Mnev,
The universality theorems on the classification problem of
configuration varieties and convex polytopes, Topology and
Geometry (Rokhlin Seminar), Lecture Notes in Math., vol. 1346,
Springer, (1988) 527-544.
- 13
- . Yu. Suvorov,
Isotopic but not rigidly isotopic plane systems of straight
lines, Topology and Geometry (Rokhlin Seminar), Lecture
Notes in Math., vol. 1346, Springer, (1988)
545-556.
- 14
-
V. F. Mazurovski
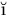 , Non-singular configurations of
, Non-singular configurations of
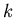 -dimensional subspaces of
-dimensional subspaces of 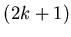 -dimensional real projective
space, Vestnik Leningrad Univ. 1990, no. 15, Mat. Mech. Astronom.
vyp. 3, 21-26 (Russian) English transl., in Vestnik Leningrad Univ.
Math.
-dimensional real projective
space, Vestnik Leningrad Univ. 1990, no. 15, Mat. Mech. Astronom.
vyp. 3, 21-26 (Russian) English transl., in Vestnik Leningrad Univ.
Math.
- 15
- Serge
 I. Khashin and Vladimir F. Mazurovski
I. Khashin and Vladimir F. Mazurovski Stable Equivalence of Real Projective Configurations, Topology of
Real Algebraic Varieties and Related Topics, Adv. in Math. Sci. 29,
Amer. Math. Soc. Transl. (2) Vol. 173 (1996) 119-140.
Stable Equivalence of Real Projective Configurations, Topology of
Real Algebraic Varieties and Related Topics, Adv. in Math. Sci. 29,
Amer. Math. Soc. Transl. (2) Vol. 173 (1996) 119-140.
- 16
- V. V. Nikulin,
Integral symmetric bilinear forms and some geometric
applications, Izv. Akad. Nauk SSSR Ser.
Mat. 43:1 (1979), 111-177.
- 17
- V. M. Kharlamov,
Non-amphicheiral surfaces of degree
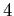 in
in
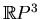 Topology
and Geometry (Rokhlin Seminar), Lecture Notes in Math., vol. 1346,
Springer (1988), 349-356.
Topology
and Geometry (Rokhlin Seminar), Lecture Notes in Math., vol. 1346,
Springer (1988), 349-356.
Oleg Viro
2000-12-29