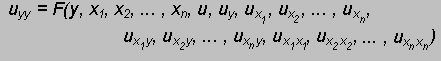The Works of Sonya Kovalevskaya
Possibly the most dazzling mathematical genius to surface among women during
the past two centuries was the highly gifted Russian, Sofia Vasilyevna
Kovalevskaya. She was born in Moscow on January 15, 1850 (3 January on
the 19th century Russian Calendar), into a family of diverse backgrounds
and talents. Sofia was destined to become a woman of great strengths veiled
by great vulnerabilities, and the contributions she made to mathematics
promise to be enduring ones.
Her doctoral dissertation, "On the Theory of Partial Differential Equations," dealt
with a rather general system of differential equations of the first order
in any number of variables. Weierstrass had already given an analogous
structure for total equations; Sonya's paper extended this to partial differential
equations. This is a remarkable contribution which was published in Crelle's
Journal in 1875. These results are still of importance today and relevant
in finding solutions to differential equations with initial conditions,
this is known as the Cauchy problem. What follows is a modern version of
what is commonly known as the
Cauchy-Kovalevskaya Theorem.
Let the partial differential equation be given in the form
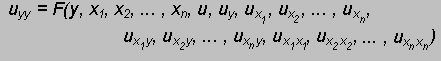

The preceding statement seems equally applicable to hyperbolic, elliptic,
and parabolic equations. However, we shall see that difficulties arise
in formulating the Cauchy problem for nonhyperbolic equations. Consider,
for instance, the Hadamard (1935) example. The problem consists of the
elliptic equation

which can be easily verified.

In addition to existence and uniqueness, the question of continuous dependence
of solution on the initial data arises in connection with the Cauchy-Kovalevskaya
theorem. It is well known that any continuous function can accurately be
approximated by polynomials. We can apply the Cauchy-Kovalevsky theorem
with continuous data using polynomial approximations only if a small variation
in the analytic data leads to a small change in the solution. For a parabolic
equation, Kovalevskaya showed that the solution may not be analytic if
the initial data are imposed on the wrong variable. Though there exist
difficulties for equations of elliptic and parabolic type, this theorem
is important for those of hyperbolic type, such as the wave equation.
Sonya also published "On the Reduction of a Definite Class of Abelian Integrals
of the Third Range," again building on Weierstrass' earlier paper on the
theory of Abelian integrals. This paper is of less importance but it consisted
of a skilled series of manipulations which showed her complete command
of Weierstrass's theory. Her other publications include a paper entitled
"Supplementary Research and Observations on Laplace's Research on the Form
of the Saturn Ring," and another paper, "On the Property of a System of
Equations."
Some time in 1881, Weierstrass gave Kovalevskaya a mathematical project
which indirectly lead her to achieve her most dazzling and important work.
The particular problem he had in mind was the set of equations which Lame'
had derived to describe the displacement of a particle in an elastic medium.
Thus in mid 1881 Sonya settled down to work on a problem which was probably
not of her own choosing, but soon after beginning, she found herself distracted
by new insight into another problem of mathematical physics which had interested
her many years earlier. This was the Euler equations which describe the
motion of a rotating rigid body. The resulting paper took around 6 years
to complete and was probably Kovalevskaya's greatest achievement. The mathematics
involved go far beyond the scope of this paper, but I will attempt a brief
description in modern notation:
The Euler equations are
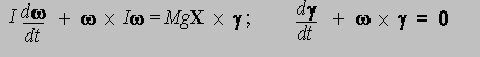

These equations form a system of six first-order differential equations
of great symmetry. Despite this great symmetry, however, the general solution
had not been found. The integrals needed for the solution were at least
hyperelliptic integrals, and probably even more complicated. The work of
Jacobi (1849) had shown that the theory of theta functions might be profitably
used to obtain a very explicit solution in a special case (X =
0) and had led Weierstrass to hope for solutions in more general cases
using the theory developed for the Jacobi inversion problem. Evidently
he had proposed this problem to Sonya while she was still a student.
Kovalevskaya's paper is assured of a permanent glory because it completes
a program implicit in the works of Euler and Lagrange - to solve in an
analytic manner the equations of motion. To do so requires cases in which
there are enough algebraic integrals to permit a reduction to quadratures,
and then a transformation of variables suitable for allowing an application
of theta functions. Also, the modern day importance of Sonya's work on
the dynamics of the top stem from her use of the study of movable poles
to determine the integrability of the dynamical system. The location of
the poles in the complex plane depends on the initial conditions for the
system of differential equations, and it has only recently been recognized
that her approach can apply to other systems. It was not even understood
at that time why her methods worked, and it is quite notable that she was
using complex analysis, a branch of mathematics that was still very much
in its infancy. It is speculated that Sonya's work in this problem may
have been inspired by Fuchs on the study of first order differential equations
in the complex plane.
The high point of Sonya's career came on Christmas Eve of 1888, when she
was presented the famous Prix Bordin of the French Academy of Sciences
in recognition of her winning memoir On the Problem of the Rotation
of a Solid Body about a Fixed Point. The rules of the competition for
such prizes dictated that each entry be submitted anonymously. The author's
name was sealed into an envelope bearing the same motto as that inscribed
on the memoir, and the envelope was not to be opened until after the competing
work won the prize. So when the jury of the Academy chose Sonya's entry,
it was in utter ignorance that the winner was a women. The excellence of
her entry was judged to be so exceptional that the value of the prize was
increased from 3,000 francs to 5,000 francs "on account of the quite extraordinary
service rendered to mathematical physics by this work." Incidentally, the
motto on Sonya's prize-winning essay was "Say what you know, do what you
must, come what may."
In the following year, the Stockholm Academy also honored Sonya with a
prize of 1,500 kroner for two more works built on her original essay. In
the same year, 1889 on the initiative of Chebyshev, Sonya was the first
woman Corresponding Member of the Imperial Academy of Sciences. Her last
published work was a short article Sur un théorème de M.
Bruns in which she gave a new, simpler proof of Bruns' theorem on a property
of the potential function of a homogeneous body. On February 10, 1891 at
the height of her mathematical powers and reputation, Sonya Kovalevskaya
died in Stockholm of influenza complicated by pneumonia.
Back to Selected Works page